R2R-Netzwerk (Carrera Autorennbahn)

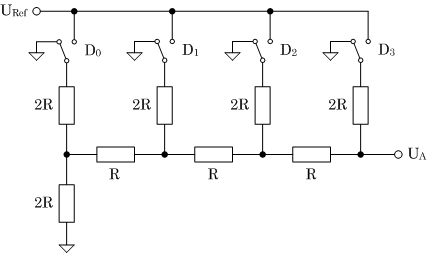
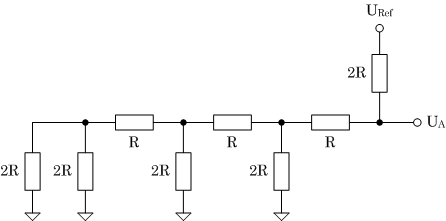
Ein R2R-Netzwerk stellt einen einfachen Weg dar, digitale Informationen in analoge umzusetzen. Dabei wird ein binär kodierter Eingangswert in eine abgestufte Ausgangsspannung gewandelt (Abbildung 1). Der Name dieses Netzwerk, das nur aus Widerständen besteht, leitet sich vom Verhältnis der verwendeten Widerstandswerte ab. Die exakten Werte der verwendeten Widerstände haben funktionell keine Bedeutung.

Abbildung 1: Prinzipieller Aufbau eines R2R-Netzwerkes

Die Schalter symbolisieren die binären Dateninformationen (D₀ – D₃). Die linke Schalterstellung (Bezugspotential) bedeutet den Wert Null für dieses Bit; die rechte Stellung des Schalters (Referenzspannung) entspricht dem Wert Eins. Die Referenzspannung (U_Ref) bestimmt die maximale Ausgangsspannung (U_A).

Funktion der Schaltung

Befinden sich alle Schalter in der linken Stellung, ist leicht zu sehen, dass die Ausgangsspannung unabhängig von der Höhe der Referenzspannung den Wert des Bezugspotentials annimmt. Für die Eingangsdaten 0000_B gilt also: U_A = 0V. Die Beschreibung für die weiteren Kombinationen der Eingangsdaten ist nach der Anzahl der Schalter gruppiert, die sich gleichzeitig in der rechten Stellung befinden.

Bestimmung der Ausgangsspannung bei maximal einem Eins-Bit

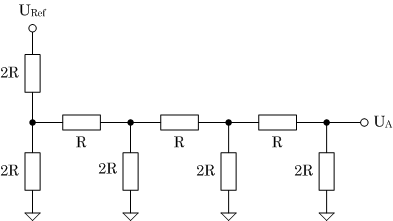
Um sich die Funktion der Schaltung in der Abbildung 1 zu verdeutlichen, schaltet man als Erstes die Schalter einzeln in die rechte Stellung und zeichnet das resultierende Widerstandswerk für jede Situation (siehe Abbildung 2).


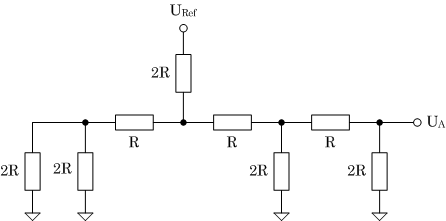
(a) Eingangsdaten 0001_B	(b) Eingangsdaten 0010_B


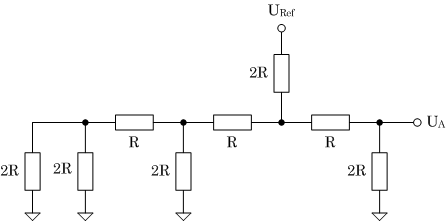
(c) Eingangsdaten 0100_B	(d) Eingangsdaten 1000_B
Abbildung 2: Resultierende Netzwerkvarianten bei nur einem Eins-Bit in den binären Eingangsdaten

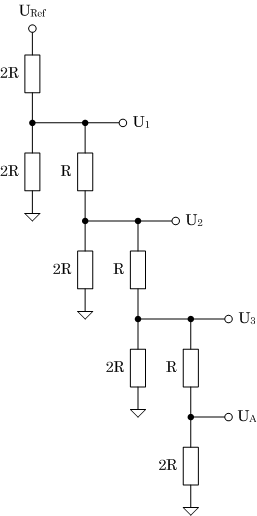
Durch die Zusammenfassung von Widerständen und die Bestimmung der Teilspannungen am unbelasteteten Spannungsteiler kann im Weiteren der Wert der Ausgangsspannung in Abhängigkeit des Wertes der Referenzspannung ermittelt werden (Abbildung 3).


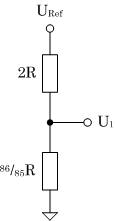U_A = 2/3 U₃	U₃ = 6/11 U₂	U₂ = 22/43 U₁	U₁ = 86/256 U_Ref
U_A = 2/3 • 6/11 • 22/43 • 86/256 • U_Ref = 1/16 U_Ref
(a) Eingangsdaten 0001_B


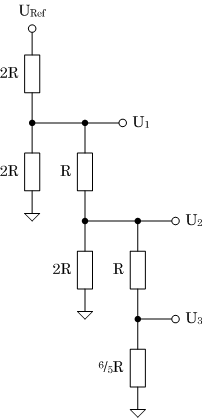
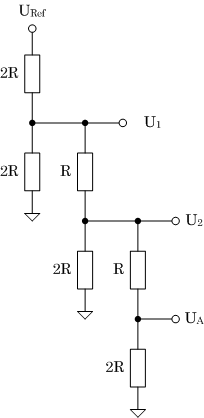
U_A = 2/3 U₂	U₂ = 6/11 U₁	U₁ = 11/32 U_Ref
U_A = 2/3 • 6/11 • 11/32 • U_Ref = 1/8 U_Ref
(b) Eingangsdaten 0010_B


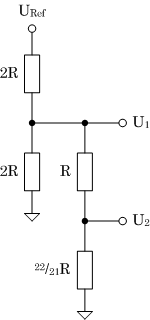
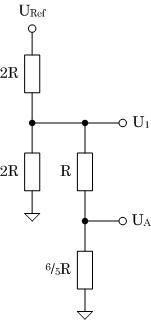
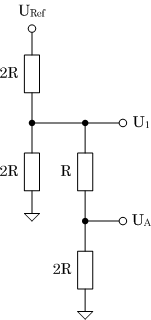
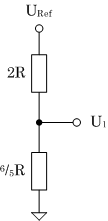
U_A = 2/3 U₁	U₁ = 6/16 U_Ref
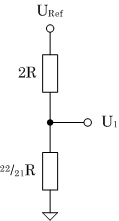
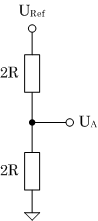
U_A = 2/3 • 6/16 • U_Ref = 1/4 U_Ref		U_A = 1/2 U_Ref
(c) Eingangsdaten 0100_B		(d) Eingangsdaten 1000_B

Abbildung 3: Bestimmung der Ausgangsspannung bei nur einem Eins-Bit in den binären Eingangsdaten

Bestimmung der Ausgangsspannung bei mehreren Eins-Bits

Die Zusammenfassung der Widerstände für die Bestimmung der Ausgangsspannung wird schwieriger, wenn mehrere Schalter gleichzeitig in die rechte Stellung geschaltet werden, da dann für einen Teil des Netzwerkes die Widerstände weder in Reihe noch parallel geschaltet sind. Am schnellsten löst man dieses Problem durch Nutzung des Superpositionsprinzips, das für lineare Systeme anwendbar ist. Dabei betrachtet man den Einfluss jeder einzelnen Spannungsquelle – jedes Schalters, der mit der Referenzspannung verbunden ist – auf die Ausgangsspannung separat und führt die ermittelten Teilergebnisse additiv zusammen. Als Beispiel dafür soll uns hier die Situation dienen, in der die Schalter D₀ und D₂ in der rechten Stellung sind – also die Kombination 0101_B (siehe Abbildung 4). Die benötigten Teilergebnisse wurden bereits im vorangegangenen Abschnitt ermittelt und werden deshalb nicht erneut diskutiert.


(a) Eingangsdaten 0101_B


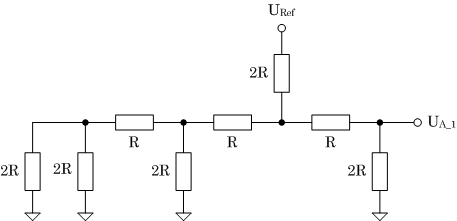(b) Einfluss des Schalters D₂ auf die Ausgangsspannung	(c) Einfluss des Schalters D₀ auf die Ausgangsspannung
U_A = U_{A_1} + U_{A_2} = (1/4 + 1/16) U_Ref = 5/16 U_Ref
Abbildung 4: Bestimmung der Ausgangsspannung mittels des Superpositionsprinzips an einem Beispiel

Wer sich lieber auf die schrittweise Umformung des Netzwerkes verlässt, kann auch den folgenden Lösungsansatz zurückgreifen. Zur Umformung wird die Stern-Dreieck-Wandlung herangezogen. Im Unterschied zur Reihen- und Parallelschaltung, die jeweils zwei externe Knoten besitzen, haben Stern- und Dreieckschaltung drei externer Knoten. Der Einfachheit halber wählen wir das gleiche Ausgangsbeispiel wie bei Nutzung des Superpositionsprinzips – die Eingangskombination 0101_B (siehe Abbildung 4a). In der Abbildung 5 ist die schrittweise Umwandlung dargestellt. Die von der Umformung betroffene Widerstandskombination wird in jedem Schritt farbig hervorgehen. Die in den Schritten 1 und 3 auftretenden Widerstände zwischen der Referenzspannung und dem Bezugspotential beschreiben die Belastung der Referenzspannungsquelle, haben aber keinen Einfluss auf die Ausgangsspannung und werden deshalb in den darauffolgenden Schritten nicht weiter betrachtet – sie sind aber in jedem Fall Bestandteil des resultierenden Netzwerkes!


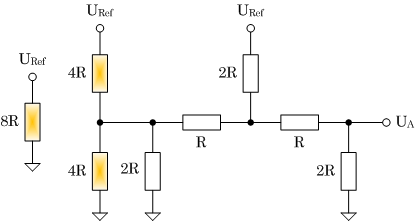(a) Schritt 1


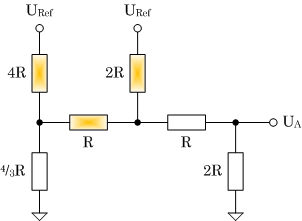(b) Schritt 2


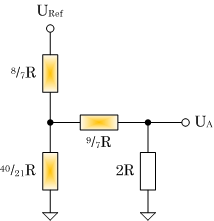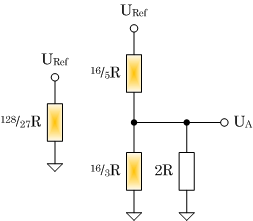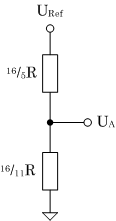(c) Schritt 3		U_A = 5/16 U_Ref
		(d) Schritt 4

Abbildung 5: Bestimmung der Ausgangsspannung durch schrittweise Umformung des Netzwerkes an einem Beispiel

Die Werte der Ausgangsspannung für die noch fehlenden zehn Kombinationen der Eingangsdaten lassen sich unter Nutzung der hier aufgeführten Methoden in gleicher Weise bestimmen. Wie sich aus den dargestellten Beispielen erkennen lässt, nimmt die Ausgangsspannung einen Wert zwischen 0V und 15/16 U_Ref in Schritten von je 1/16 U_Ref an.